Ausarbeitung im Rahmen eines Projekts "Neue Technologien"

Eike Teiwes
LOGO im Mathematikunterricht
1987

1 Didaktische Analyse und Sachanalyse

Im Mathematikunterricht kann der Schüler den Rechner als Benutzer und Gestalter kennenlernen. Ein Computersystem, das den Mathematikunterricht als pädagogisches und fachliches Hilfsmittel begleiten, aber auch selbst Gegenstand einer Erörterung sein soll, muß mehreren Bedingungen genügen. Eine Betrachtung der Eigenschaften des Programmiersystems LOGO - ergänzt durch ausgewählte Unterrichtsbeispiele - zeigt, daß dieses den gestellten Anforderungen voll gerecht wird.

Der Computer - einst als Rechenmaschine eingeführt, dann als Datenverarbeitungsanlage verbreitet - ist nun als "Denkmaschine" im Vormarsch begriffen. Während sich immer vielfältigere Anwendungsmöglichkeiten für Computer finden, gerät der Mensch zunehmend in die Defensive. Er sieht seine Position in mehrfacher Hinsicht - bei seiner Arbeit, in seiner Privatsphäre, in seinem Selbstwertgefühl - gefährdet. In dieser kritischen Phase des Einzugs einer universalen Maschine in unsere Gesellschaft reicht es nicht aus, nur die technischen Möglichkeiten des Computers zu diskutieren, um die anstehenden Probleme zu lösen. Die beginnende Umwälzung erfordert dringend eine Auseinandersetzung des Menschen mit sich selbst. "Die angemessene Aufnahme der Herausforderung durch die Computerentwicklung könnte doch statt in der möglichst weitgehenden Übernahme der bereitgestellten Möglichkeiten und Anpassung an dadurch »automatisch« sich anbahnende Entwicklungen gerade darin bestehen, daß wir tiefer und umfassender als je die Sinnfrage stellen müssen, daß wir erst recht danach fragen müssen, was wir eigentlich wollen, welche »Visionen für ein Morgen« wir eigentlich haben." [Köhler]

Mit Blick auf diese grundsätzliche Fragestellung darf der Einsatz des Computers im Mathematikunterricht nicht allein aus fachdidaktischen Überlegungen heraus begründet oder abgelehnt werden. Vielmehr ist im einzelnen abzuwägen, inwieweit auch der Mathematikunterricht einen Beitrag für eine Auseinandersetzung mit der Informationstechnik leisten kann.

"Die Schule muß sich dem Problemfeld Informationstechnik und Medien zuwenden, weil nur sie als allgemeine Bildungsinstitution technische Grundbildung mit inhaltlich-kritischer geistiger Auseinandersetzung wirksam verbinden kann." [Hurrelmann/Hurrelmann]

2 Informationstechnologische Bildung in der Schule

"In der Informationstechnischen Grundbildung sollen Schülerinnen und Schüler Erfahrungen in verschiedenen Rollen - als Betroffener, als Benutzer und auch als Gestalter - beim Umgang mit informationstechnischen Systemen sammeln. [...]
Vier Themenbereiche bestimmen den Unterricht für die informationstechnische Grundbildung: Anwendungsbereich, Technischer Bereich, Algorithmischer Bereich, Gesellschaftlicher Bereich.
Der Unterricht in der informationstechnischen Grundbildung sollte in wenigen, komplexeren Unterrichtseinheiten erteilt werden. In jeder Unterrichtseinheit sollten, in der Regel von einem im Zentrum stehenden Anwendungsfall ausgehend, möglichst alle Themenbereiche erschlossen werden." [MNU]

Der Einsatz des Computers sollte immer dadurch begründet sein, daß er eine pädagogisch erwünschte Lernsituation schafft und das Erreichen des fachlichen Unterrichtsziels begünstigt oder daß er selbst als Gegenstand einer Betrachtung dient. Vorteile und Nachteile des Rechnereinsatzes sollten die Schüler in möglichst "normalen" Unterrichtssituationen erfahren und anschließend diskutieren. Die bei der Übertragung auf ein Rechnersystem unumgängliche Reduktion von Information und die in der Begrenztheit logischen Denkens begründete eingeengte Interpretationsweise sollten bei jeder Gelegenheit - auch im Mathematikunterricht - deutlich gemacht werden.

Die Schüler sollen die Möglichkeiten des Computers sachlich einzuschätzen lernen und sich der prinzipiellen Einschränkungen dieses Geräts bewußt werden. Die kritische Behandlung von Computerlösungen ist insbesondere im Zusammenhang mit der vom Menschen im einzelnen nicht mehr nachvollziehbaren Verarbeitung großer, vielleicht personenbezogener Datenmengen angezeigt. Aber: "Kann die Schule an Zwergen auf die Beherrschung von Riesen vorbereiten?" [Bauersfeld] Der Gefahr einer Verharmlosung der Computertechnik im überschaubaren, kleinen Rahmen der Schule kann vielleicht dadurch begegnet werden, daß der Rechnereinsatz bewußt modellhaft erfolgt, orientiert an der außerschulischen "echten" Datenverarbeitung, aber doch distanziert und offen für ergänzende Erkenntnisse, die draußen "vor Ort" gewonnen werden sollten.

Jeder Schüler muß "ein Gespür dafür entwickeln, welche Gefahren in einer exzessiven Computernutzung liegen, denn diese sind das eigentliche Problem für ihn und die Gesellschaft." [Köhler] Eine sachgerechte Verwendung von Computern in der Schule ist dafür unabdingbare Voraussetzung.

Um die prinzipiellen Grenzen des Computers umfassend aufzuzeigen, sind verschiedene Wege zu verfolgen:

Wenn der Computer problembezogen als Werkzeug benutzt wird, lassen sich die Auswirkungen seines Einsatzes direkt beobachten und diskutieren. Voraussetzung für eine kritische Beurteilung ist jedoch die genaue Kenntnis des Problemgegenstandes, dessen Bearbeitung mit herkömmlichen Methoden bekannt sein muß. Auch bei der Programmierung in einer problemorientierten Sprache findet der Rechner als Werkzeug Verwendung.
Der Mystifizierung des Computers kann durch den Bau einfacher technischer Computermodelle begegnet werden. An diesen überschaubaren, "begreifbaren" logischen Schaltungen lassen sich wesentliche Elemente digitaler Datenverarbeitung im Schülerexperiment aufzeigen.

Der Unterricht über und mit dem Computer muß von einer philosophischen Auseinandersetzung über Welt und Leben begleitet werden. "Es ist nötig, daß der Schüler nicht nur als Intellekt, sondern als ganzer Mensch vom Gegenstand angeredet und auch erreicht, ja betroffen wird. Nur dann kann er spüren oder gar sich bewußt machen, daß die »Disziplin« des Faches auch ihn selber, den Menschen, einschränkt; wodurch allein er eben den bestimmten fachlichen Aspekt der Wirklichkeit zu Gesicht bekommt, von dem er sich nun reflexiv zu distanzieren lernt." [Wagenschein] Die Förderung ganzheitlichen Denkens ist Teil einer Erziehung zu verantwortlichem Handeln.

Es wäre zu wünschen, daß die Konfrontation des Kindes mit den Neuen Technologien solange aufgeschoben wird, bis sich sein auf verschiedenen, möglichst unmittelbaren Erfahrungen begründetes Weltbild stabilisiert hat. Aber die Auseinandersetzung mit der modernen Technik beginnt früh und außerhalb der Schule. Die Schule muß dem Kind helfen, diese zunächst fremdartigen Eindrücke einzuorden, Abstand zu halten und die eigene Integrität zu bewahren. Sie muß sich in kritischer Distanz auch mit dem Computer beschäftigen, den Umgang mit ihm versachlichen und einer Anpassung an derartige Gerate oder gar einer Abhängigkeit von ihnen begegnen. "Die schulische Vermittlung von Kind und Computer kann möglicherweise an der kindlichen Spiellust anknüpfen. [...]
Möglicherweise enthält die kindliche und jugendliche Begeisterung für den Computer ein spielerisches Element, das verhindern könnte, daß der Umgang mit dem Computer zu einer dauerhaften Festlegung der Wirklichkeitserfahrung wird." [Danner]

3 Computer im Mathematikunterricht

Durch den Einsatz von Computern ist eine "Fortentwicklung und Bereicherung des Mathematikunterrichts" [MNU] zu erwarten. "Mittelfristig wäre ein grundsätzliches Überdenken der Curricula notwendig hinsichtlich der Ziele, Methoden und Inhalte, und zwar aufgrund
- der veränderten Rolle von Mathematik in Beruf, Gesellschaft und Wissenschaft,
- der neuen Möglichkeiten des Lernens und Lehrens, die der Computer als Arbeitsmittel und Medium im Unterricht ermöglicht." [MNU]

Fachdidaktisch bedeutsam ist eine Stärkung der Auffassung von Mathematik als Tätigkeit.

"Für den Einsatz des Computers im Mathematikunterricht sehen wir folgende Schwerpunkte:

Einsatz von Rechnern als Werkzeug für die Bearbeitung von Problemen, d.h. Computer als Arbeitsmittel und nicht primär als simples Demonstrationsmedium,

verstärkte Nutzung der Computer-Grafik als Arbeitsmittel, als Verständnishilfe und zur Motivation,

stärkere Einbeziehung experimentellen Arbeitens in den Mathematik-Unterricht, z.B. zum Auffinden mathematischer Gesetzmäßigkeiten und mathematischer Modelle,

Herausstellen und Förderung des Anwendungsbezugs,

Förderung des selbständigen und kooperativen Arbeitens,

kritische Reflexion und Bewertung des Rechner-Einsatzes." [MNU]

Es lassen sich folgende Schwerpunkte erkennen:

pädagogisch: An die Spiellust des Kindes anknüpfend besteht die Chance, seinen Forscherdrang aufzugreifen und experimentelles Arbeiten zu fördern. Selbständiges Entdecken und Ausprobieren stärkt die Identifikation mit dem Produkt und begünstigt die Entwicklung in persönlichen Erfahrungen verankerten Wissens. Während der Lehrer eher in die Rolle eines Beraters rückt, bietet der Rechner aufgrund seiner Rückmeldungen geeignete Hilfestellungen und ermöglicht ungestraftes Lernen aus Fehlern. Eine sinnvoll organisierte Arbeit im Team kann auch die Kommunikationsfähigkeit und die Kooperationsbereitschaft fördern.

fachdidaktisch: Beim selbständigen Programmieren wird Mathematik als Tätigkeit erlebt. "Mathematisches und Computermodell werden in ständiger Wechselwirkung miteinander entwickelt. Ideen für die Problemlösung werden möglichst unmittelbar in die Programmiersprache übertragen und im Prozeß des »strukturierten Wachstums« der Programmierumgebung einverleibt. Erproben, Verbessern, Verfeinern und Verallgemeinern sind grundlegende Arbeitstechniken." [Hoppe] Das Programm bildet schließlich als extern repräsentiertes, "lauffähiges" Modell die Problemlösestrategie nach und bietet Anlaß zur Erprobung und Diskussion. Das Herausfinden der zugrunde liegenden Strukturen und Funktionsmechanismen bietet einen direkten, "persönlichen" Zugang zum formalen und mathematischen Denken. In einer geeigneten Sprachumgebung - wie sie LOGO darstellt - werden die Schüler zu seiner selbständigen Konstruktion und Formulierung mathematischer Begriffe geführt. Eine solche Terminologie ist Voraussetzung für die Selbstreflexion und für Gespräche über den Prozeß der Ergebnisgewinnung. Wenn - wie bei LOGO - die Möglichkeit besteht, eine problemspezifische Sprachumgebung vorzugeben, kann das Erforschen auf höherer Ebene beginnen, so daß auch Simulationen und graphische Veranschaulichungen in Schüleraktivität eingebettet sind.

informationstechnologisch: Im Mathematikunterricht lernt der Schüler den Computer als Benutzer und Gestalter kennen. Dabei erfährt er durch eigenes Handeln die bei der Modellbildung sich vollziehende Reduktion und Verfremdung, zugleich erlebt er ein Programm als einmal gelungene und nun durch den Computer immer wieder abrufbare, möglichst allgemeine Problemlösung. Während der technische Bereich - vielleicht von der Einführung in digitales Rechnen abgesehen - im Mathematikunterricht unberücksichtigt bleiben muß, kann der gesellschaftliche Bereich in einzelnen Unterrichtsprojekten (etwa zur Versicherungsmathematik o.ä.) mit einbezogen werden.

4 Lernziele

Die Zielsetzungen des beschriebenen Einsatzes des Computers im Mathematikunterricht zeigen große Übereinstimmung mit den allgemeinen Zielen dieses Fachs. Nach Winter [zitiert in Wittmann] soll der Mathematikunterricht dem Schüler Möglichkeit geben,
- schöpferisch tätig zu sein,
- rationale Argumentation zu üben,
- die praktische Nutzbarkeit der Mathematik zu erfahren und
- formale Fertigkeiten zu erwerben.

Auch die Verfeinerung dieser Ziele des Mathematikunterrichts deutet auf die Möglichkeit einer gewinnbringenden Integration des Computers in den Fachunterricht hin.

"Kognitive Strategien

1. Der Schüler soll lernen. Situationen (mathematischer und besonders auch real-umweltlicher Art) zu mathematisieren
(1) Situationen mit mathematischen Mitteln erfassen und darstellen
(2) Daten gewinnen (Experimentieren, Zählen, Messen, Schätzen)
(3) Strukturelle Zusammenhänge aufdecken und formulieren (m.a.W. Bildung einer mathematischen Struktur bzw. - im Fall einer Realsituation - eines mathematischen Modells)
(4) Sachrelevante Problemstellungen aufgreifen bzw. selbst finden
(5) Daten im Hinblick auf Lösung der Probleme verarbeiten
(6) Lösungen situationsadäquat interpretieren und diskutieren

2. Der Schüler soll lernen, sich forschend-entdeckend und konstruktiv zu betätigen
(1) Vermutungen (z.B. über Beziehungen, Muster, Strukturen, ...) aufstellen
(2) Lösungs- und Beweisideen entwickeln, Lösungswege planen
(3) komplexere Handlungsabläufe logisch geordnet in Teilschritte gliedern
(4) über die gegebene Information hinausgehen
(5) eine Situation variieren, fortsetzen und übertragen
(6) Verallgemeinerungen erkennen und formulieren
(7) Probleme konstruieren

3. Der Schüler soll lernen zu argumentieren
(1) sich an Vereinbarungen (z.B. Definitionen) holten
(2) allgemeine Aussagen am Spezialfällen testen (Beispiele-Gegenbeispiele)
(3) begründen, folgern, beweisen
(4) Begründungen auf Stichhaltigkeit prüfen, Scheinargumente aufdecken
(5) mathematische Überlegungen bezüglich ihrer Bedeutung bewerten

Grundwissen und Grundtechniken

4. Der Schüler soll Grundkenntnisse und Grundtechniken zur Verarbeitung mathematischer Informationen einschließlich deren Anwendung erlernen
(1) Mathematische Instrumente sachgemäß bedienen
(2) Bildliche Darstellungen (Situationsskizzen, Diagramme, Zeichnungen, ...) und Fachsprache verwenden
(3) Nach vorgegebenen Regeln korrekt operieren
(4) Algorithmen (zum Konstruieren, Sortieren, Ordnen, Zuordnen, Berechnen, ...) korrekt anwenden; Algorithmen in Computerprogramme überführen
(5) Definitionen, Sätze und Einzelaussagen anwenden
(6) logische Techniken und Beweistechniken anwenden" [Wittmann nach Winter]

Dieser Eindruck wird bei Betrachtung der effektiven Ziele des Mathematikunterrichts bestätigt:

"Der Schüler sollte danach
1. Freude und Interesse an der Mathematik und eine positive Einstellung zum Fach entwickeln
2. Selbstvertrauen bei mathematischer Arbeit haben
3. mit Begeisterung, Zielbewußtheit und Konzentration arbeiten und Neues lernen wollen
4. Bereitschaft zum Mitmachen entwickeln
5. in der Mathematik geistige Anregung und Befriedigung finden
6. Freude und Stolz über den erfolgreichen Abschluß mathematischer Untersuchungen empfinden
7. die Mathematik als relevant und nützlich verstehen und ihren Wert für die Gesellschaft würdigen
8. die (relative) Klarheit mathematischer Begriffe und die (relative) Sicherheit mathematischer Erkenntnisse würdigen." [Wittmann]

Von den allgemeinen Zielsetzungen des Mathematikunterrichts her drängt sich der Einsatz des Computers demnach geradezu auf, wohl weil der Schüler - aktiv am Rechner tätig - die Notwendigkeit formalen Denkens und überlegten Handelns unmittelbar einsieht. Bei Betrachtung einzelner Unterrichtsbeispiele wird zwar deutlich, daß auch ohne Computereinsatz eine vergleichbare, offene Lernsituation geschaffen werden kann. Da ein derartiger Unterricht zur Zeit aber eher untypisch ist, stellt das Werkzeug Computer wohl auch in pädagogischer Hinsicht eine Herausforderung dar.

"Zweifellos ermöglichen die neuen Medien Formen des Lernens, die die Selbsttätigkeit der Schüler herausfordern. Sie enthalten Chancen der Veranschaulichung, der Individualisierung, der Selbstkontrolle, der Selbstdisziplinierung zu präziser Aufgabenformulierung und logischer Folgerichtigkeit des Denkens [...]. Aber sie taugen keinesfalls als universelle Lehrmittel." (Hurrelmann/Hurrelmann]

5 Sachinformation: Das Programmiersystem LOGO

Ein Computersystem, das den Mathematikunterricht im beschriebenen Sinn als pädagogisches und fachliches Hilfsmittel begleiten, aber auch selbst Gegenstand der Auseinandersetzung mit aktueller Informationstechnik sein soll, muß mehreren Bedingungen genügen. Das Programmiersystem LOGO scheint z.Z. den Anforderungen am besten gerecht zu werden. "In der BRD steht der Computereinsatz im Mathematikunterricht vorrangig unter dem Gesichtspunkt der Programmierung numerischer Verfahren. [...] LOGO erschließt dem Computer im Mathematikunterricht neue Anwendungsfelder wie Grafik, Symbol Verarbeitung und die Rekonstruktion mathematischer Strukturen. Es ist möglich und wünschenswert, daß dadurch der allgemeinere Aspekt der Modellbildung gegenüber dem reinen Algorithmieren an Bedeutung gewinnt." [Hoppe]

Eine Betrachtung der Eigenschaften dieses "Endbenutzerwerkzeugs" soll seine Eignung besonders für den Mathematikunterricht verdeutlichen.

LOGO stellt ein vollständiges Programmiersystem dar. Ein einfacher Texteditor und einfache Befehle zur Speicherung von Daten und

Programmen auf Diskette sind so in die Programmiersprache eingebettet, daß ihre Benutzung ohne langwierige Einführung schnell erlernt werden kann. Ohnehin zeichnet sich das LOGO-System durch einen leichten Zugang aus. Ein Anfänger - mit nur wenigen Befehlen vertraut - kann bereits in der ersten Übungsstunde konkrete Aufgabenstellungen bearbeiten, den Rechner also als Werkzeug kennenlernen, das er nun - bei Bedarf und Interesse - durch Variation oder Erweiterung seiner Problemstellung weiter "erobern" kann.

LOGO ist interaktiv: Die Eingaben des Benutzers werden sofort kontrolliert und ausgeführt bzw. durch brauchbare Fehlermeldungen kommentiert, so daß die Programmentwicklung erheblich unterstützt wird. "Der Rechner ist unmittelbarer Bestandteil der Lernumgebung. Der Problemlöseprozeß entspricht einem Regelkreis, in dem das »feedback« über die Rückmeldungen des Rechners erfolgt. [...] Das Lernen aus Fehlern und die instrumentelle Hilfestellung durch den Rechner [gelten] als didaktisch wertvolle Möglichkeiten, die der Lernende ungehindert nutzen soll." [Hoppe] Interessant ist diese Art der Programmierung euch aus fachdidaktischer Sicht: "Mit dem interaktiven Programmieren [verbindet sich] notwendigerweise ein experimentelles Arbeiten im Umgang mit formalen oder formalisierten Darstellungen, [die dem Schüler] sonst eher auf deduktivem Wege zugänglich gemacht werden. Interaktives Programmieren unterstützt so das konstruktive Problemlösen", das in enger Verbindung mit der Modellbildung zu sehen ist. [Hoppe]

LOGO ist modular und erweiterbar: Aufbauend auf den vorgegeben Sprachkonstrukten kann der Benutzer durch Entwicklung eigener Prozeduren weitere Sprachelemente schaffen, die vollständig in das LOGO-System eingebettet werden. Jede Prozedur ist ein unabhängiger Baustein, der von außen mit Daten versorgt werden und seinerseits Daten zurückgeben kann. Jede Prozedur kann - zusammen mit denen, die sie aufruft - für sich getestet werden. Ein LOGO-Programm kann daher als ein Baukasten von Prozeduren beschrieben werden, die in Wechselwirkung mit dem abstrakten Modell entwickelt und aufeinander bezogen wurden.

Für den Unterricht kann der Lehrer einen problembezogenen Sprachkontext vorbereiten und auf Diskette ablegen. Als Musterbeispiel für eine solche Lernumgebung ist die Igelgraphik bereits in das System integriert. Für den Mathematikunterricht müssen weitere für größere Problemzusammenhänge geeignete Lernumgebungen bereit gestellt werden. Zurecht warnt allerdings Bauersfeld vor zu großen Erwartungen und bemängelt, daß das Vermittlungsmedium zu einer sehr begrenzten Auswahl von mathematischen Inhalten zwingt, die zudem verdeckt vorstrukturiert sind. "Daß die Lernenden »die Wirklichkeit formen können, in der sie arbeiten wollen« und daß sie »die aktiven Konstrukteure und Architekten ihres eigenen Lernprozesses werden können« (Papert), erweist sich als eine der großen Verheißungen Paperts, die nur in äußerst begrenzten, disparaten und geschlossenen Handlungsbereichen der Möglichkeit nach einlösbar wird." [Bauersfeld]

Die Vorstellung von dem, was wie mit einem Computer bearbeitet werden kann, wird durch die benutzte "Modellvorstellung vom Computer" bestimmt. "Ein solches »Modell vom Computer« ersetzt die komplexeren physikalischen Vorgänge durch stark vereinfachte vor- oder nachvollziehbare Reaktionsmuster" [Hoppe] LOGO bietet einfache Modellvorstellungen vom Computer an: Die Igelgeometrie "ist reich an Metaphern und daher besonders gut geeignet, einen anschaulichen Zugang zum Arbeiten mit LOGO zu vermitteln." [Hoppe] So überzeugend dieses von Papert geprägte anthropomorphe Modell ist, bei jüngeren Schülern ist zu befürchten, daß die "menschlichen Züge" dieses "Igels" die Grenze zwischen Mensch und Maschine unnötig verwischen. Eine Auseinandersetzung mit dieser Frage wird hier nicht nur angeregt, sie ist unabdingbar.

Für den Mathematikunterricht von größerer Bedeutung ist das Operatormodell, das sich in der funktionalen Schreibweise von LOGO niederschlägt. "Funktionale Sprachen betonen stärker die Objekte, wahrend bei imperativen (d.h. anweisungsorientierten) Sprachen mehr die Prozesse im Vordergrund stehen. Das ermöglicht z.T. »mathematiknahe« Formulierungen; schließlich gehört der Begriff der Funktion zu den fundamentalen Begriffen der Mathematik." [Schuppar] So läßt sich beispielsweise die in der Abbildungsgeometrie übliche Schreibweise in LOGO direkt übernehmen.

LOGO erweist sich in dieser Hinsicht als zukunftsorientiert: Während LOGO einerseits die bekannten Züge imperativen Programmierens (Fragestellung: "Wie soll das Programm arbeiten ?") trägt, kann es zugleich das moderne deklarative Konzept (Fragestellung: "Was soll das Programm tun ?") vorbereiten.

LOGO ist eine rekursive Sprache, so daß in der Mathematik übliche rekursive Begriffsbildungen direkt in LOGO formuliert werden können. Beim Problemlösen stellt die Rekursion einen Spezialfall der Problemreduktionsmethode dar. "Der Vorteil der rekursiven Methode liegt darin, daß nicht der gesamte Ablauf der Problemreduktion bedacht und festgelegt werden muß, sondern eine eher statische Beschreibung des allgemeinen Falles vermittels eines einfacheren gegeben wird. Dabei wird die Lösung des vereinfachten Problems im Sinne einer »black box« verwendet." [Hoppe]

Im übrigen kann auch in LOGO (durch Rücksprung auf eine Marke in derselben Prozedur) iterativ programmiert werden. Ganz im Gegensatz zur Rekursion liegt dieser Art der Wiederholung ein maschinennahes Denken zugrunde, das in der Regel nicht erwünscht ist.

LOGO verarbeitet Listen und ist deshalb auch für nicht-numerische Problemstellungen geeignet. Mit Listen läßt sich jede beliebige Datenstruktur aufbauen. Das Listenkonzept "löst sich von der speicherplatz-orientierten Vorstellung der Daten und vermeidet überdies lästige Dimensionierungsanweisungen." [Menzel]

Weitere Eigenschaften von LOGO:

LOGO ist in deutscher Sprache verfügbar. Dem Vorteil eines einheitlichen, dem Problem zugewandten Sprachgebrauchs steht dabei allerdings als Nachteil die Gefahr der Gewöhung an "schlechtes" Deutsch gegenüber.
LOGO ist graphikfähig. Der Übergang vom Textmodus zum Graphikmodus und umgekehrt erfolgt problemlos.
LOGO unterscheidet zwar die Datentypen Liste und Wort (sowie Zahl als spezielles Wort), erfordert jedoch keine Typvereinbarung. So kann eine Funktion BETRAG PARAMETER geschrieben werden, die selbst den Typ des aktuellen Parameters bestimmt und eine entsprechende Aktion veranlaßt, also z.B. bei BETRAG "GERHARD die Anzahl der Buchstaben des Wortes, bei BETRAG [3 4] die Länge des Vektors mit den Koordinaten 3 und 4 und bei BETRAG - 12.3 den Betrag der Zahl zurückgibt.
LOGO unterscheidet deutlich zwischen dem Variablennamen und dem zugehörigen Wert. Mit SETZE "X 5 wird dem Namen "X der Wert 5 zugeordnet, und durch WERT "X wird der dem Namen "X zugeordnete Wert abgefragt.
Dieses Variablenkonzept erlaubt die Unterscheidung von Wert- und Variablenparametern von Prozeduren.
LOGO unterscheidet beim Prozeduraufruf globale und lokale Variablen.

Einige Einschränkungen sind im wesentlichen darauf zurückzuführen, daß in (heute noch gebräuchlichen, den Ausstattungsempfehlungen nicht gemäßen) Computern mit 64kB-Speicher nur ein abgemagertes LOGO-System Platz findet:

LOGO ist langsam, das ist in der Schule aber von geringer Bedeutung.
Die Rechenergebnisse besitzen eine geringe Genauigkeit. Auch das kann als Problemaufhänger durchaus nützlich sein.
Es bietet dem Benutzer nur einen geringen Arbeitsspeicher, was z.B. bei rekursiven Prozeduraufrufen zum Ausstieg führen kann.
Einige Logo-Versionen bieten keine formatierte Ausgabe.
Programme können im Editor nicht optisch strukturiert werden.
Der Dateizugriff ist unzulänglich bei einigen Systemen.

6 Beispiele für den Mathematikunterricht

Die für den Unterricht interessanten Eigenschaften von LOGO werden anhand der folgenden Programme noch einmal hervorgehoben. Die vorgestellten Beispiele können an geeigneter Stelle im Unterricht aufgegriffen werden. Auf eine ausführliche Beschreibung der Einbettung in den Unterricht wird verzichtet.

1. Beispiel: Igelgraphik

a) Experimentieren mit den Grundbefehlen

Die Igelgrafik ist geeignet, den Anfänger mit dem Programmieren vertraut zu machen. Die Befehle VORWAERTS, RUECKWAERTS, LINKS und RECHTS (zusätzlich vielleicht STIFTAUF und STIFTAB) reichen aus, um jede beliebige Figur darzustellen, z.B. ein Rechteck:

VORWAERTS 20
LINKS 90
VORWAERTS 40
LINKS 90
VORWAERTS 20
LINKS 90
VORWAERTS 40

b) Unterprogramm/Spracherweiterung (Programm RECHTECK1)

Der LERNE-Befehl erlaubt es, verschiedene Befehle unter einem neuen Wort zusammenzufassen. Nach Eingabe von LERNE RECHTECK 1 wird automatisch ein Texteditor bereitgestellt. Der Benutzer kann das Sichtfenster nun als "Notizblatt" betrachten, auf dem er die LOGO-Befehle nach und nach entwickelt, ergänzt, korrigiert usw. Diese Befehlsliste speichert das LOGO-System beim Verlassen des Editors mit der Meldung "RECHTECK1 GELERNT" unter dem Namen RECHTECK1 ab. Mit dem Aufruf RECHTECK1 kann die notierte Befehlsfolge anschließend identifiziert und ausgeführt werden.

PR RECHTECK1
VORWAERTS 20
LINKS 90
VORWAERTS 40
LINKS 90
VORWAERTS 20
LINKS 90
VORWAERTS 40
ENDE

c) Verallgemeinerung (Programme RECHTECK2. RECHTECK3)

Bei wiederholter Ausführung der Prozedur RECHTECK 1 zeigt sich, daß die Figur unterschiedlich (jeweils um 90° gedreht) dargestellt wird. Die unmittelbare Reproduzierbarkeit des Befehls wird durch Anfügen des Befehls LINKS 90 wird erreicht.

PR RECHTECK2
VORWAERTS 20
LINKS 90
VORWAERTS 40
LINKS 90
VORWAERTS 20
LINKS 90
VORWAERTS 40
LINKS 90
ENDE

PR RECHTECK3
WIEDERHOLE 2 [VORWAERTS 20 LINKS 90 VORWAERTS 40 LINKS 90]
ENDE

Mit Hilfe des neuen Wortes RECHTECK2 bzw. RECHTECK3 (und den Befehlen VORWAERTS, LINKS, RECHTS, vielleicht auch STIFTAUF, STIFTAB) können nun schnell und bequem komplexere Figuren, z.B. "Manhattan" oder "meine Initialen" entworfen werden.

d) Unterprogramm mit Parametern (Programm RECHTECK4)

Um Figuren verschiedener Größe darstellen zu können, wird man wie beim VORWAERTS- oder LINKS-Befehl erst beim Prozeduraufruf eine Maßzahl angeben wollen. Im Programmtext werden dazu Platzhalter, z.B. :A und :B, eingeführt. Der Doppelpunkt wird zunächst damit begründet, daß der Name von einer Prozedur namens A unterscheidbar sein soll. Die Nennung der Parameter in der Kopfzeile der Prozedur sichert die Eindeutigkeit der Zuordnung: Beim Aufruf RECHTECK4 60 30 der Prozedur mit der Kopfzeile PR RECHTECK4 :A :B ist :A gleich 60 und :B gleich 30.

PR RECHTECK4 :A :B
WIEDERHOLE 2 [VORWAERTS :A LINKS 90 VORWAERTS :B LINKS 90)
ENDE

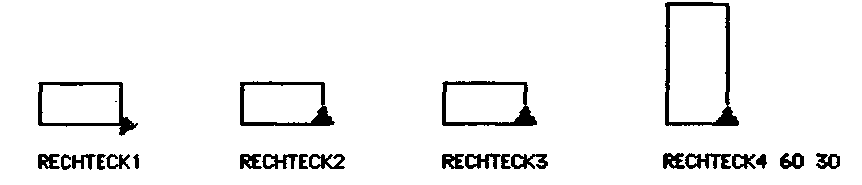
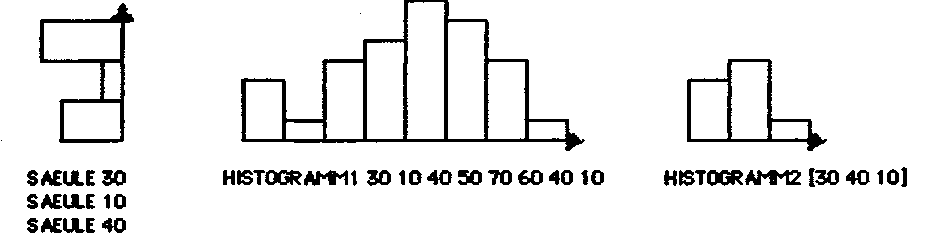
e) Problemlösung (Programme SAUELE, HISTOGRAMM1)

Diese Kenntnisse werden nun aufgegriffen, um ein anwendungsnahes Problem zu bearbeiten, etwa um eine statistische Verteilung graphisch darzustellen. Die Aufgabe, ein Histogramm für z.B. acht Merkmale darstellen zu lassen, können die Schüler selbständig bearbeiten (etwa in Form der hier angegebenen Programme).

PR SAEULE :N
VORWAERTS 20
LINKS 90
VORWAERTS :N
LINKS 90
VORWAERTS 20
LINKS 90
VORWAERTS :N
LINKS 90
VORWAERTS 20
ENDE

PR HISTOGRAMM1 :A :B :C :D :E :F :G :H
BILD
STIFTHOCH
AUFXY -80 0
STIFTAB
AUFKURS 90
SAEULE :A
SAEULE :B
SAEULE :C
SAEULE :D
SAEULE :E
SAEULE :F
SAEULE :G
SAEULE :H
ENDE

f) Verallgemeinerung der Problemlösung. Liste und Rekursion (Programme HISTOGRAMM, HISTOGRAMM2)

Die Schüler sollten bereits erkannt haben, daß ein Programm möglichst allgemein einsetzbar sein sollte. Zwei Einschränkungen sind in der bisherigen Problemlösung erkennbar:
- Die Merkmalswerte können im Einzelfall zu groß oder zu klein sein.
- Die Anzahl der Merkmale wird in der Regel von 8 verschieden sein.

Die Lösung im ersten Fall bietet eine prozentuale Darstellung der Merkmalswerte (siehe dazu das 2. Beispiel). Die Bewältigung des zweiten Problems erfordert weitere Kenntnisse von LOGO:

Der nachfolgenden Prozedur HISTOGRAMM wird als Parameter eine Liste übergeben, in der die Merkmalswerte aufgeführt sind. Eine Liste stellt eine Folge von beliebig vielen Elementen dar, bei der die Reihenfolge wohl // beachtet wird. Um nun das zugehörige Histogramm zu gewinnen, wird man zunächst die Säule zu dem ersten Wert in der Liste zeichnen, also z.B. bei der Liste [20 10 40 50 70 60 40 10] zunächst eine Säule der Höhe 20. Dann ist das nächste Histogramm für die Restliste, also für die Liste [10 40 50 70 60 40 10l, zu zeichnen usw. In LOGO formuliert lautet die Problemlösung:

PR HISTOGRAMM :LISTE
SAEULE ERSTES :LISTE
HISTOGRAMM OHNEERSTES :LISTE
ENDE

In dieser Form sollte des Programm getestet werden. Es stellt sich heraus, daß die Programmausführung am Schluß mit der Fehlermeldung "ERSTES MAG NICHT ALS EINGABE" abbricht. Das ist klar, denn es kann kein erstes Element mehr gefunden werden, wenn die Liste schließlich "abgearbeitet" (leer) ist. Also wird die Problemlösung um eine Zeile erweitert:

WENN :LISTE = [ ] DANN RUECKKEHR

Um das Histogramm in der Mitte des Sichtschirm zu platzieren, wird das Unterprogramm HISTOGRAMM in ein Rahmenprogramm HISTOGRAMM2 eingebunden.

PR HISTOGRAMM2 :LISTE
BILD
STIFTHOCH
AUFXY -80 0
STIFTAB
AUFKURS 90
HISTOGRAMM :LISTE
ENDE

PR HISTOGRAMM :LISTE
WENN :LISTE = [] DANN RUECKKEHR
SAEULE ERSTES :LISTE
HISTOGRAMM OHNEERSTES :LISTE
ENDE

2. Beispiel: Igelgraphik

Die Darstellung des ersten Beispiels mag den Eindruck erwecken, daß sich ein stark lehrerzentrierter Unterricht entwickeln könnte. Dieselbe Problemstellung wird deshalb noch einmal verkürzt auf andere Weise dargestellt. Im Unterricht können "schnelle" Schüler gleich auf diesen Weg überwechseln, wenn er ihnen besser gefällt. Andere Schüler können diese Lösung aufgreifen, wenn sie sich nach ersten Erfahrungen sicherer fühlen. Schwächere Schüler können sich auf den ersten Lösungsweg konzentrieren und ihn variieren.

a) Experimentieren mit den Grundbefehlen. Prozeduren (Programme N.ECK 1, N.ECK2, N.ECK3)

Wiederholtes Vorwärtsgehen und Drehen bewirkt eine "Kreis"-Bewegung. Um ein Tortenstück zu zeichnen, muß in regelmäßigen Abständen ein Radius eingezeichnet werden. Die Länge wird durch Probieren gefunden.

PR N.ECK1
WIEDERHOLE 36 [VORWAERTS 10 LINKS 10]
ENDE

PR N.ECK2
WIEDERHOLE 36 [VORWAERTS 10 LINKS 95 VORWAERTS 56 RUECKWAERTS 56 RECHTS 85]
ENDE

PR N.ECK3
WIEDERHOLE 180 [VORWAERTS 2 LINKS 91 VORWAERTS 58 RUECKWAERTS 58 RECHTS 89]
ENDE

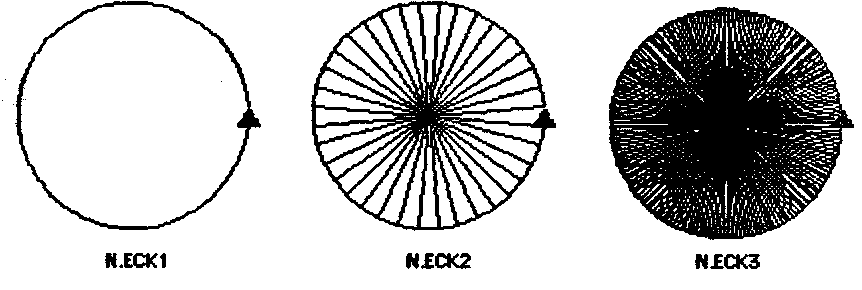
b) Problemlösung (Programme SEKTOR, KREISDIAGRAMM1)

Ein Kreisdiagramm setzt sich aus mehreren, in der Regel verschieden großen Sektoren zusammen. Mit SEKTOR wird ein Sektor bestimmter ßröße abgesteckt. KREISDIAGRAMM benutzt dieses Unterprogramm, um nacheinander verschiedene Merkmalswerte graphisch darzustellen. Die Summe aller Merkmalswerte muß 360 (einer Volldrehung entsprechend) ergeben. Es wird gleich die rekursive Lösung mit einer Liste als Parameter angegeben.

PR SEKTOR :N
WIEDERHOLE :N [VORWAERTS 1 LINKS 1]
LINKS 89.5 VORWAERTS 56 RUECKWAERTS 58 RECHTS 89.5
ENDE

PR KREISDIAGRAMM1 :LISTE
IF :LISTE = [] RUECKKEHR
SEKTOR ERSTES :LISTE
KREISDIAGRAMM 1 OHNEERSTES :LISTE
ENDE

c) Verallgemeinerung der Problemlösung. Funktion und rekursive Funktion (Programme PROZENTSATZ, KREISDIAGRAMM, SUMME, KREISDIAGRAMM2)

In KREISDIAGRAMM wird die Größe eines Sektors nun durch den Prozentsatz des entsprechenden Merkmal wertes an der Summe aller Merkmalswerte festgelegt. Der Prozentsatz wird von einer Funktion PROZENTSATZ berechnet. Eine Funktion ist eine Prozedur, die einen Wert zurückgibt, der anschließend weiterverarbeitet werden kann.

Beim Aufruf KREISDIAGRAMM [3 4 2 5 4] 18 muß der Benutzer die Summe der Merkmalswerte selbst berechnen und als zweiten Parameter angeben. Die Berechnung dieser Summe kann der Rechner aber selbst durchführen: Wenn die Liste leer ist, ist die Summe aller ihrer Werte 0. Andernfalls erhält man die Summe aller Werte, wenn man zum Wert des ersten Elements die Summe aller restlichen Werte addiert.

PR KREISDIAGRAMM2 :LISTE
KREISDIAGRAMM :LISTE SUMME :LISTE
ENDE

PR KREISDIAGRAMM :LISTE .SUMME
WENN :LISTE = [] DANN RUECKKEHR
SEKTOR 3.6*PROZENTSATZ ERSTES :LISTE :SUMME
KREISDIAGRAMM OHNEERSTES :LISTE :SUMME
ENDE

PR PROZENTSATZ :X :SUMME
RUECKGABE :X * 100 / :SUMME
ENDE

PR SUMME :LISTE
WENN :LISTE = U DANN RUECKGABE 0
RUECKGABE (ERSTES :LISTE) + SUMME OHNEERSTES :LISTE
ENDE

Bei der Funktion SUMME wird deutlich, daß die Rekursion zu einer eher statischen Beschreibung einer Problemlösung führt.

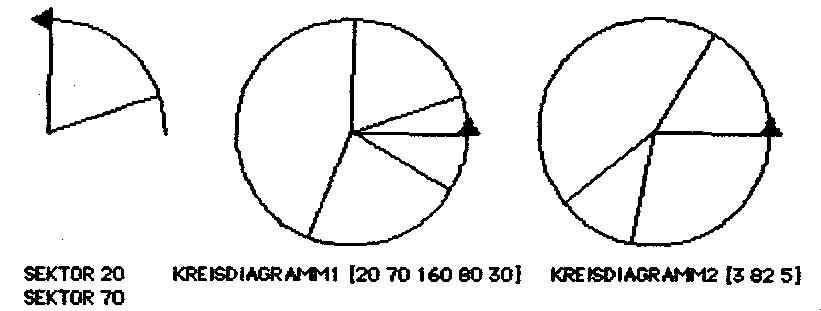
Anmerkung: Und natürlich geht es noch ganz anders. Der "Igel" wird in das Zentrum des Kreises gebracht. Um das Kreisdiagramm zu :LISTE zu zeichnen, dreht er sich um ERSTES :LISTE nach links, trägt einen Radius an und kehrt zum Mittelpunkt zurück. Dieses wiederholt sich dann rekursiv mit OHNEERSTES :LISTE, bis die Liste leer ist. Anschließend wird noch ein "Kreis" mit dem gewählten Radius - Probieren führt zum Ziel - um die entstandene Figur gelegt:

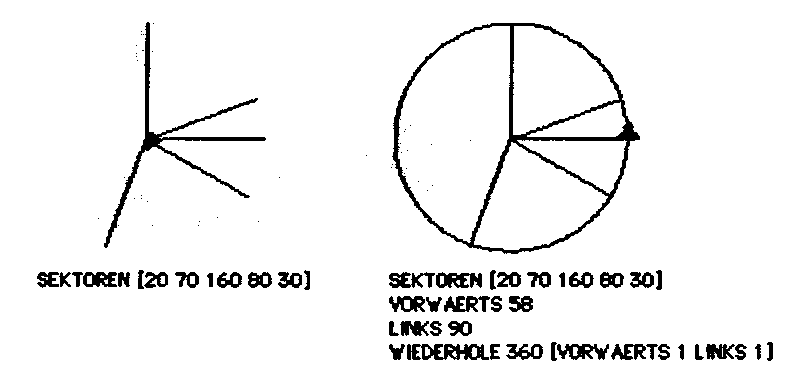
3. Beispiel: Abbildungsgeometrie

Die Abbildungsgeometrie bereichert den Mathematikunterricht in vielfacher Hinsicht: Die Schüler sind gefordert, handwerklich sauber und genau zu arbeiten. Sie entwickeln anhand zeichnerischer Konstruktionen ihr geometrisches Vorstellungsvermögen und lernen, Abbildungen formal zu beschreiben. Der Einsatz des Computers als Hilf s- ' mittel gefährdet diese persönlichen Lernerfahrungen, wenn er zu früh erfolgt. Da die Abbildungsgeometrie aber in mehreren Schuljahren behandelt wird, liegt der Schwerpunkt schließlich stärker auf der abstrakten Ebene und zeichnerische Konstruktionen werden - z.B. bei Verkettungen -zunehmend langwierig und unergiebig. Denn stellt der Rechner mit LOGO als Programmiersystem ein nützliches Werkzeug dar.

Als Datenobjekte sollen Vielecke, als Abbildungen sollen Verschiebungen, Spiegelungen, Drehungen und Streckungen in LOGO beschrieben und auf dem Graphikschirm dargestellt werden.

a) Zunächst ist die Datenstruktur für Vielecke festzulegen. Ein Vieleck ist ein geschlossener Streckenzug und durch eine bestimmte, im allgemeinen unterschiedliche Anzahl von Punkten, die in bestimmter Reihenfolge verbunden sind, festgelegt. Jeder Punkt kann durch eine zweielementige Liste beschrieben werden, alle zu einem Vieleck gehörigen Punkte - in der vorgesehenen Reihenfolge - als Liste solcher "Punkt"-Listen. Z.B. beschreibt [[20 0] [60 0] [40 60]] ein gleichschenkliges Dreieck.

b) Die Darstellung erfolgt, indem zunächst mit angehobenem Stift der Anfangspunkt des Streckenzugs angesteuert wird und dann mit gesenktem Stift der Streckenzug selbst abgefahren wird. Zur Abwechslung werden die Programme in einer englischsprachigen LOGO-Version, die sich auch in der Syntax teilweise von der bisher benutzten unterscheidet, angegeben.

TO zeichne :vieleck
IF EMPTYP :vieleck [STOP]
PENUP
SETPOS FIRST :vieleck
PENDOWN
zeichne 1 BUTFIRST LPUT FIRST :vieleck :vieleck
END

TO zeichne1 :punktliste
IF EMPTYP :punktliste [STOP]
SETPOS FIRST :punktliste
zeichne 1 BUTFIRST :punktliste
END

c) Von den genannten Abbildungen wird nur die Verschiebung betrachtet. Die Prozeduren für Punktspiegelungen, Streckungen und Drehungen bezogen auf den Ursprung sind in gleicher Weise aufgebaut. Grundsätzliche (mathematische) Schwierigkeiten ergeben sich bei den Drehungen um Winkel, die von 0°, 90°, 180°, 270° verschieden sind. Die mathematischen Voraussetzungen für diese Abbildungen können erst in Klasse 10 im Rahmen der Trigonometrie erarbeitet werden.

Für jede Abbildung wird eine Funktion definiert, so daß z.B. die Befehlsfolge

MAKE "abc [[20 0] [60 0] [40 60]]
zeichne :abc
zeichne verschoben (-40) 20 Spiegelung :abc
MAKE "def Spiegelung verschoben (-40) 20 :abc
zeichne :def

möglich wird. Die letzte Zuweisung schreibt der Mathematiker fast identisch in der Form:

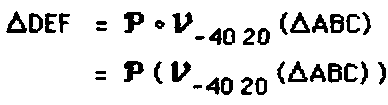
Da die Abbildungen geradentreu sind, entsteht jede Bildfigur dadurch, daß alle in der ursprünglichen Punktliste aufgeführten Eckpunkte abgebildet und miteinander verbunden werden.

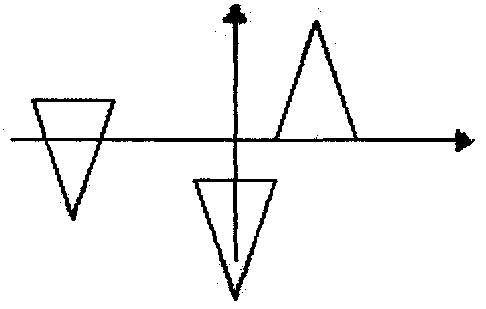
Solche Aufgaben, bei denen alle Elemente einer Liste in irgendeiner Form verändert werden sollen, treten immer wieder auf. Die Lösung erfolgt - in rekursiver Form - immer nach demselben Muster:

1. Eine leere Liste wird unverändert zurückgegeben.
2. Bei einer nichtleeren Liste wird das erste Element abgetrennt und mit ihm die gewünschte Operation ausgeführt. Dann wird es wieder als erstes Element in die zwischenzeitig entsprechend veränderte Restliste eingefügt.

In LOGO ergibt sich die folgende Beschreibung dieses Vorgehens:

TO veraendert :liste
IF EMPTVP :liste [OUTPUT [] ]
OUTPUT FPUT (Operation FIRST :liste) (veraendert BUTFIRST :liste)
END

FPUT :element :liste gibt die Liste :liste vorn um das Element :element erweitert zurück.

"operation" stellt irgendeine auf die Elemente der Liste wirkende Operation dar. Auch die Verschiebung eines Vielecks läßt sich nach diesem Lösungsmuster ausdrücken:

TO verschoben :dx :dy :liste
IF EMPTYP :liste [OUTPUT []]
OUTPUT FPUT (punktv :dx :dy FIRST :liste ) (verschoben :dx :dy BUTFIRST :liste)
ENDE

Die Verschiebung ein Punktes erfolgt so::

TO punktv :dx :dy :punkt
OUTPUT LIST (FIRST :punkt + :dx) (LAST :punkt + :dy)
END

d) Wenn die Abbildungen (Punkt-)Spiegelung, Streckung und Drehung bezogen auf den Ursprung bekannt sind, können sie leicht auf einen beliebigen Punkt (x|y) bezogen werden:

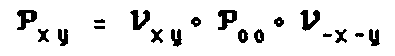
TO gespiegelt :X :Y :figur
OUTPUT verschoben :X :Y gespiegelt00 verschoben (-:X ) (-:Y) :figur
END

"gespiegelt00" beschreibt darin die Spiegelung am Ursprung.

e) Ein Vieleck kann auch durch seine Kanten beschrieben werden, die z.B. durch Polarkoordinaten (Winkel p und Länge r) angegeben werden. ABC ergibt sich dann als [ [0 20] [ [0 40] [108.435 63.246] [251.565 63.246] ] ]. Dieses Beispiel zeigt allerdings bereits, daß die Größen p und r nur in speziellen Fällen ohne Kenntnisse aus der Trigonometrie bestimmt werden können. Die Lage der Figur wird durch einen zusätzlichen Polarvektor, der zum Anfangspunkt des Streckenzugs führt, festgelegt.

TO zeichne :figur
IF EMPTYP :figur [STOP]
PENUP
SETHEADING 90 - FIRST FIRST :figur
FORWARD LAST FIRST rfigur
PENDOWN
zeichne1 LAST :figur
END

TO zeichne1 :liste
IF EMPTYP :liste [STOP]
SETHEADING 90 - FIRST FIRST :liste
FORWARD LAST FIRST :liste
zeichne1 BUTFIRST :liste
END

Weitere Darstellungsarten sind möglich. Bei der Realisierung verschiedener Abbildungsprozeduren zeigt sich die eine oder andere Datenstruktur überlegen. Die Schüler sollten die Wahl der Struktur selbst treffen und die Konsequenzen daraus durch den Vergleich mit anderen Lösungen erfahren. Aufgabe des Lehrers ist es, einerseits den Informationsaustausch zwischen den erfolgreich arbeitenden Gruppen zu sichern und andererseits den übrigen Gruppen gezielte Hilfen zu geben.

4. Beispiel: Mathematische Funktionen

Durch den Einsatz des Computers wird es möglich, Algorithmen für die Berechnung von Potenzfunktionen, von Exponential- und Logarithmusfunktionen, von trigonometrischen Funktionen u.a. zu realisieren (s. dazu Engel und Schuppar). Hier werden verschiedene LOGO-Programme für die Berechnung der Potenzen xⁿ (n € N) vorgestellt und diskutiert.

xⁿ =	x · x · x · ... · x =	1 · (x · x · x · ... · x)
	n Faktoren	n Faktoren

Also ergibt sich xⁿ durch n-malige Multiplikation von 1 mit x. Die folgenden Prozeduren POTENZ1 und POTENZ2 zeigen, daß die in anderen Programmiersprachen üblichen iterativen Berechnungen auch in LOGO möglich sind:

PR POTENZ 1 :X :N
SETZE "ERG l
MARKE: WENN :N = 0 DANN RUECKGABE :ERG
SETZE "ERG :ERG * :X
SETZE "N:N-1
GEHE "MARKE
ENDE

PR POTENZ2 :X :N
SETZE "ERG 1
WIEDERHOLE :N [SETZE "ERG :ERG*:X]
RUECKGABE :ERG
ENDE

Die in LOGO übliche rekursive Berechnung der Potenz bezieht sich auf die Darstellung:

xⁿ = 1,	wenn n=0
xⁿ = x •x^n-1,	wenn n>0

PR POTENZ3 :X :N
WENN :N = 0 DANN RUECKGABE 1
RUECKGABE :X * POTENZ3 :X (:N-1)
ENDE .

Die Ausführung dieses Unterprogramms bricht bei größerem n wegen mangelnden Speicherplatzes ab, denn bei der rekursiven Berechnung muß in jeder aufgerufenen Prozedur bei der Abarbeitung der vorletzten Zeile der Wert von x (und andere Systemgrößen) zwischenspeichert werden, um später - nach Erhalt des Ergebnisses xn-1 - die vorgesehene Multiplikation durchführen zu können. In der folgenden Prozedur wird diese Einschränkung dadurch aufgehoben, daß das Zwischenergebnis stets weitergereicht wird. Allerdings muß beim Aufruf von POTENZ4 als dritter Parameter stets 1 übergeben werden.

PR POTENZ4 :X :N :ERG
WENN :N = 0 DANN RUECKGABE :ERG
RUECKGABE POTENZ4 :X (:N-1) (:X*:ERG)
ENDE

Die optimale Lösung folgt am Schluß. Die Beziehung x^m • x_n = ^xm+n ausnutzend ergibt sich (mit [z] als größtes Ganzes von z)

xⁿ = 0	für n = 0
xⁿ = (x^2)[n/2]	für n > 0 und n gerade
xⁿ= x • (x^2)[n/2]	für n > 0 und n ungerade

Diese Beziehung läßt sich In LOGO direkt niederschreiben:

PR POTENZ5 :X :N
WENN :N = 0 DANN RUECKGABE 0
PRUEFE (REST :N 2) = 0
WENNWAHR RUECKGABE POTENZ5 (:X * :X) (DIV :N 2)
WENNFALSCH RUECKGABE :X * POTENZ5 (:X * :X) (DIV :N 2 )
ENDE

Während bei der Berechnung von z.B. 1.0011000 die Prozeduren POTENZ3 und POTENZ4 - käme es nicht zum Programmabbruch - jeweils 1001 mal aufgerufen würden, benötigt die Prozedur POTENZ5 wegen des zugrunde liegenden Halbierungsverfahrens nur elf Aufrufe. Ähnliche Verfahren können auch für andere mathematische Funktionen angegeben werden.

5. Beispiel: Problemlöser

Computer können auch zum Entwurf von Problemlösungen herangezogen werden. Soll etwa in Klasse 10 nach Vorgabe von drei oder mehr Größen eines Dreiecks eine weitere berechnet werden, so kann sich folgender Dialog mit dem Rechner abspielen:

BERECHNUNG VON DREIECKSGROESSEN
WELCHE DER GROESSEN A, B, C, ALPHA, BETA, GAMMA SIND GEGEBEN?
>A B BETA
WELCHE GROESSE IST GESUCHT?
>C
BERECHNE ALPHA MIT SINUSSATZ A B ALPHA BETA
BERECHNE GAMMA MIT WINKELSUMMENSATZ ALPHA BETA GAMMA
BERECHNE C MIT SINUSSATZ C A GAMMA ALPHA

Da des zugehörige Programm flexibel auf unterschiedliche Vorgaben reagieren kann, ist seine Leistungsfähigkeit beachtlich. Um so erstaunlicher ist es, daß es durch einen einfachen Algorithmus beschrieben wird: Die gegebenen Größen werden in einer Liste festgehalten. Das Programm erweitert solange diese Liste unter Benutzung vorgegebener Formeln, die auch durch Listen repräsentiert werden, bis die gesuchte Größe darunter ist. Die Formeln - zusammengestellt in der Prozedur SUCHE - stellen die Informationsbasis des Systems dar. Die Reihenfolge ihrer Nennung beeinflußt die Effektivität des Lösungsweges nicht unerheblich. Eine Formel ist genau denn brauchbar, wenn alle bis auf eine der in ihr genannten Größen bekannt sind. Denn kann die fehlende Größe aus den anderen berechnet und in die Liste der gegeben Größen aufgenommen werden.

Im Unterricht sollte man ausnahmsweise nicht erst des Programm entwickeln und es anschließend testen. Interessanter wird es sein, die Schüler zunächst mit den "Fähigkeiten" des Computers zu konfrontieren, um dann die Grundidee des Algorithmus zu erarbeiten und ihre Einfachheit offen zu legen. Besondere Aufmerksamkeit sollte der Strategie, der Auswahl und Reihenfolge der Formeln, gewidmet werden.

PR HILFE
DRUCKEZEILE [BERECHNUNG VON DREIECKSGROESSEN]
DRUCKEZEILE l --------------------------------- ]
DRUCKEZEILE [WELCHE DER GROESSEN A, B, C, ALPHA, BETA, GAMMA]
DRUCKEZEILE [SIND GEGEBEN?]
DRUCKE [>]
SETZE "GEGEBEN EINGABE
DRUCKEZEILE [WELCHE GROESSE IST GESUCHT?]
DRUCKE [>]
SETZE "GESUCHT ERSTES EINGABE SUCHE
ENDE

PR SUCHE
WENN ENTHALTEN :GESUCHT :GEGEBEN DANN AUSSTIEG
BENUTZE "WINKELSUMMENSATZ [ALPHA BETA GAMMA]
BENUTZE "SINUSSATZ [A B ALPHA BETA] BENUTZE "SINUSSATZ [B C BETA GAMMA]
BENUTZE "SINUSSATZ [C A GAMMA ALPHA] BENUTZE "KOSINUSSATZ [ABC ALPHA]
BENUTZE "KOSINUSSATZ [ABC BETA] BENUTZE "KOSINUSSATZ [ABC GAMMA]
DRUCKEZEILE [ES FEHLEN WEITERE ANGABEN]
ENDE

PR BENUTZE :NAME :FORMEL
WENN NICHT UMFANG SCHNITT :GEGEBEN :FORMEL = (UMFANG :FORMEL) - 1 DANN RUECKEHR
SETZE "GEGEBEN SATZ :GEGEBEN DIFFERENZ :FORMEL:GEGEBEN
(DRUCKEZEILE [BERECHNE] DIFFERENZ :FORMEL :GEGEBEN [MIT] :NAME :FORMEL)
SUCHE
ENDE

Nicht aufgeführt werden hier die Hilfsprozeduren

PR ENTHALTEN :ELEMENT :LISTE
PR SCHNITT :LISTE1 :LISTE2
PR DIFFERENZ :LISTE1 :LISTE2
PR UMFANG :LISTE

7 Literatur

Für eine Einarbeitung in das Thema werden die mit • gekennzeichneten Bücher bzw. Aufsätze empfohlen.

• Abelson. Harald. Einführung in LOGO. Vaterstetten: IWT, 1983.

Bauersfeld, Heinrich. "Die Andersartigkeit der Computererfahrung - oder die neue "Neue Mathematik" ". Bildschirm Jahresheft III.

Danner, Helmut. "Für das Leben lernen wir!" - Zum Verhältnis von Schule, Kind, Computer und Wirklichkeit". Bildschirm Jahresheft Hl.

Deutscher Verein zur Förderung des mathematischen und naturwissenschaftlichen Unterrichts e.V. (MNU) Hg. "Empfehlungen und Überlegungen zur Gestaltung von Lehrplänen für den Computer-Einsatz im Unterricht der allgemeinbildenden Schulen". MNU 38. Heft 4 (1985).

Engel. Arthur. Elementarmathematik vom algorithmischen Standpunkt. Stuttgart: Klett, 1977.

• Hoppe, Heinz Ulrich. LOGO im Mathematik-Unterricht. Vaterstetten: IWT, 1985.

Hoppe, Heinz Ulrich u. Löthe, Herbert. Problemlösen und Programmieren mit LOGO. Stuttgart: Teubner. 1964.

Hurrelmann, Bettina u. Claus. "Ein neues Lernfeld für Schüler und Lehrer - Für eine kritische Auseinandersetzung". Bildschirm Jahresheft III.

• Köhler, Hartmut. "Computer als Herausforderung - zur Sklavenarbeit? Fragen zur Computerwelt und möglichen Reaktionen durch allgemeinbildende Schulen". MNU 38, Heft 1 u. 2(1985).

Menzel, Klaus. LOGO in 100 Beispielen. Stuttgart: Teubner, 1985.

Schuppar, Bertold. LOGO-Programmierkurs für Commodore 64 LOGO und Terrapin LOGO (Apple II). Braunschweig/Wiesbaden: Vieweg, 1985.

• Teiwes, Eike. Logo im Unterricht. Hannover: Schroedel, 1986.

Wagenschein, Martin. Ursprüngliches Verstehen und exaktes Denken. Bd.l und Bd. II. Stuttgart: Klett, 1970.

Wittmann, Erich. Grundfragen des Mathematikunterrichts. Braunschweig/Wiesbaden: Vieweg, 1981.

Eike Teiwes LOGO im Mathematikunterricht 1987