Regression
Darstellung von Datenpunkten
Datenpunkte festlegen
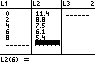
Punkte in einem Diagramm darstellen
Fenster festlegen
Regressionsmodelle
lineares Modell
quadratisches Modell
kubisches Modell
Modell vierten Grades
logarithmisches Modell
Exdivonentialmodell
Potenzmodell
logistisches Modell
sinusförmiges Modell
f(x)=ax+b
f(x)=ax2+bx+x
f(x)=ax3+bx2+cx+d
f(x)=ax4+...+dx+e
f(x)=a+b·ln(x)
f(x)=a·bx
f(x)=a·xb
f(x) =
f(x)=a·sin(bx+c)+d
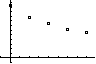
4:LinReg(ax+b)
5:QuadReg
6:CubicReg
7:QuartReg
9:LnReg
0:ExdivReg
A:PwrReg
B:Logistic
C:SinReg
Lineares Wachstum: Lineare Regression
Ansatz: f(x)=ax+b
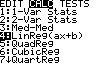
Die Datenpaare stehen in den Listen L1 und L2.
Der Funktionsterm soll unter Y1 abgespeichert werden.
Der Funktionsterm soll unter Y1 abgespeichert werden.
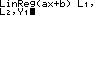

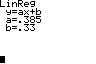
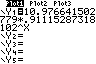
Exponentielles Wachstum: Exponentielle Regression
Modell: f(x) = a·bx
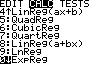
Stat Calc 0:ExpReg
Stat Calc 0:ExpReg
Daten aus erstem Beispiel
Die Datenpaare stehen in den Listen L1 und L2.
Der Funktionsterm soll unter Y1 abgespeichert werden.
Die Datenpaare stehen in den Listen L1 und L2.
Der Funktionsterm soll unter Y1 abgespeichert werden.


Also ist
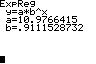
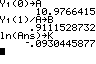
f(t) ≈ 10,97·0,91x
≈ 10,97·e-0,093·x
f(t) ≈ 10,97·0,91x
≈ 10,97·e-0,093·x
Prognose für x=12:
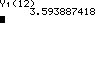
Beschränktes Wachstum: Regression mit einer verketteten Funktion
Die Datenpaare stehen in den Listen L1 und L2.
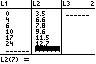
Plot mit
xmin=-1
ymin=0
Zoom 9:ZoomStat
Windowxmin=-1
ymin=0

Modell: f(x) = S − a·bx
Es ist f(x) = v(u(x))
mit u(x) = a·bx und v(x) = S−u(x)
Wir wählen willkürlich S = 14 und ...
Es ist f(x) = v(u(x))
mit u(x) = a·bx und v(x) = S−u(x)
Wir wählen willkürlich S = 14 und ...
... bestimmen die exponentielle Regression für
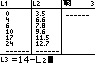
u(x) = 14 − f(x) = a·bx
mit den Werten in L3.
mit den Werten in L3.

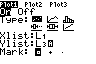
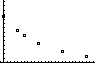

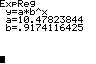
Also ist u(x) ≈ 10,5∙0,92x und
f(x) = 14 ≈ u(x) – 14 − 10,5∙0,92x
Mit einem anderen Wert für S ergeben sich andere Werte für a und b, aber derselbe Funktionsterm f(x).
Mit einem anderen Wert für S ergeben sich andere Werte für a und b, aber derselbe Funktionsterm f(x).
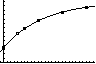
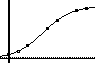
Logistisches Wachstum: Logistische Regression
Die Datenpaare stehen in den Listen L1 und L2.
Einstellung Zoom 9:ZoomStat
Einstellung Zoom 9:ZoomStat
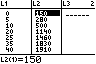
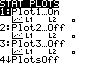

Der Funktionsterm soll unter Y1 abgespeichert werden.

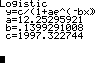
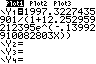


Also ist
f(x) ≈
≈
f(x) ≈
≈
"gebr. rat. Glockenkurve": Regression mit einer verketteten Funktion
Modell:
f(x) =
Es ist f(x) = v(u(x))
mit u(x) = a·x²+c und v(x) = .
Es ist f(x) = v(u(x))
mit u(x) = a·x²+c und v(x) = .
Die Datenpaare stehen in den Listen L1 und L2.
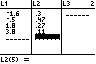
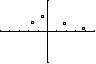
Für u(x) = a·x²+c gilt das quadratische Modell.
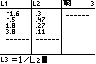
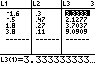
Die Datenpaare stehen in den Listen L1 und L3.
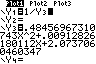
Der Funktionsterm soll unter Y3 abgespeichert werden.
Der Funktionsterm soll unter Y3 abgespeichert werden.
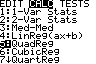
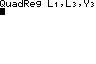
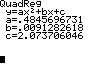
In Y3 steht der Term für u(x).
1/Y3 liefert f(x).
Wegen des linearen Terms b·x in Y3 ist dr Graph nicht x-achsensymmetrisch.
1/Y3 liefert f(x).
Wegen des linearen Terms b·x in Y3 ist dr Graph nicht x-achsensymmetrisch.
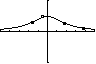
Um x-Achsensymmetrie zu erhalten, kann man die Wertepaare doppelt eintragen, also (xi|yi) und (-xi|yi).