Verteilungen
Binomialverteilung
|
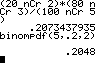
n = 50; p = 0,2 B50;0,2 (X=10) B50;0,2 (X≤10) |
DISTR 0:binompdf(50,.2,10) DISTR A:binomcdf(50,.2,10) |
|
|
n = 50; p = 0,2 B50;0,2 (X>10) B50;0,2 (X<10)
|
1 - DISTR A:binomcdf(50,.2,10) DISTR A:binomcdf(50,.2,9) |
|
|
n = 50; p = 0,2 B50;0,2 (10≤X≤20) |
DISTR
A:binomcdf(50,.2,20) |
|
Tabellen zur Binomialverteilung (Wahrscheinlichkeitsverteilung, Summenverteilung)
|
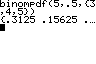
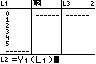
n = 5; p = 0,2 Tabelle |
MEM 4:ClrAllLists STAT 1:Edit L1 L2
L3 anschließend Quit |
|
|
n = 5; p = 0,2 Tabelle in Kurzform |
Blättern mit Pfeiltasten
|
|
|
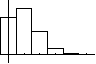
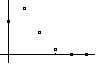
n = 5; p = 0,2 Plot |
k in L1, P(X=k) in L2 STATPLOT
1:Plot GRAPH ZOOM 9:ZoomStat
|
|
Allgemeine Näherungsformel von De Moivre-Laplace für Binomialverteilung
|
n
= 30, p = 0,4 |
|
|
|
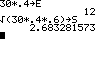
n = 30, p = 0,4 P(k1≤X≤k2)≈ Φ - Φ P(20≤X≤25) |
30 * .4 STO E √( 30 * .4 * .6 STO S nach Formel DIST 2:normalcdf( (19.5-E)/S , (25.5-E)/S ) einfacher DIST 2:normalcdf( 19.5 , 25.5 , E , S ) |
|
Vereinfachte Näherungsformel von De Moivre-Laplace für Binomialverteilung
|
n
= 500, p = 0,7 |
|
|
|
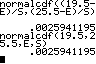
n=500 und p=0,7 P(k1≤X≤k2) ≈ Φ - Φ P(360≤X≤400) |
500 * .7 STO E √( 500 * .7 * .3 STO S nach Formel DIST 2:normalcdf( (360-E)/S , (400-E)/S ) einfacher DIST 2:normalcdf( 360 , 400 , E , S ) |
|
|
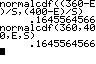
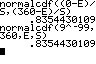
n=500 und p=0,7 P(X ≤ 360) |
nach Formel DIST 2:normalcdf( (0-E)/S , (360-E)/S ) einfacher DIST 2:normalcdf( 10 ^ -99 , 360 , E , S ) |
Hinweis: 9-99 ≈ -∞ |
|
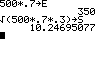
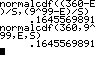
n=500 und p=0,7 P(360 ≤ X) |
nach Formel DIST 2:normalcdf( (360-E)/S , (9^99-E)/S ) einfacher DIST 2:normalcdf( 360 , e ^ 99 , E , S ) |
Hinweis: 999 ≈ ∞ |
Hypergeometrische Verteilung
|
Anzahl N
= 50 |
|
|
|
Für
die Berechnung mehrerer Werte und deren Summierung lohnt die
Erstellung einer Funktion. |
|
|
|
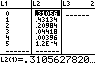
Für die Berechnung mehrerer Werte und deren Summierung lohnt die Erstellung einer Tabelle. N = 50, M = 10, n = 5 P(X=k) ≈ 0,2580 |
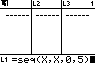
LIST OPS 5:seq( X , X, 0 , 5 )
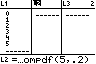
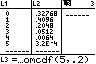
( 10 MATH PRB 3:nCr L1 ) ( 50 MATH PRB 3:nCr ( 5 − L1 )) / ( 50 MATH PRB 3:nCr 5) oder mit der definierten Funktion VARS Y-VARS 1:Function 1:Y1( L1 ) LIST MATH 5:sum( L2, 2 ,4 )
ZOOM 9:ZoomStat |
|
|
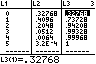
P(X≤3) = P(X=i) |
Achtung: Die Zahlen stehen in der Liste L2 auf den Plätzen 1 bis 4. LIST MATH sum( L2, 1 , 4 ) |
|
|
Vergleich mit Binomialverteilung
|
B 20; 0.6 unter Plot2 |
|
|
Die Varianz der hypergeometrischen Verteilung ist kleiner als die Varianz der Binomialverteilung. Erklärung 1: Wenn wenige Treffer vorliegen, steigt dadurch die Wahrscheinlichkeit für einen Treffer beim nächsten Wurf (und umgekehrt). Erklärung
2: Je mehr Kugeln ohne Zurücklegen gezogen werden, desto
genauere Informationen liegen über die restlichen noch in
der Urne enthaltenen Kugeln vor. Die Streuung der
Zufallsvariablen X verringert sich dadurch. |
|
|
|
|
|
|
|
Für n ≤ kann die hypergeometrische Verteilung durch eine Binomialverteilung mit p = angenähert werden. Erklärung: Wenige Ziehungen oder Ziehungen aus einer großen Grundgesamtheit verändern das "Mischverhältnis" wenig. N = 100, M = 20, n = 5, k Treffer 5 ≤ , also z.B. P(X=2)≈B5;0,2 (X=2) |
|
|
Poisson-Verteilung
|
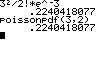
n = 600, p = 0,005 < 0,1 μ = n·h = 3 < 6 P(X=2) = ≈ 0,61 |
nach Formel ... mit Funktion ...
|
|
|
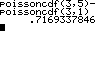
N = 600, p = 0,005 P(X=2) ≈ 0,72 |
|
|
Geometrische Verteilung
|
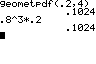
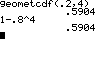
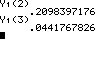
p = 0,2 P(X=4) genau
4 Versuche bis zum Treffer; |
mit Funktion ... nach Formel ... |
|
|
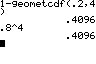
p = 0,2 P(X≤4) höchstens
4 Versuche bis zum Treffer; |
|
|
|
p = 0,2 P(X>4) = 1−P(X≤4) mehr
als 4 Versuche bis zum Treffer; |
|
|
Normalverteilung (stetiges Merkmal)
|
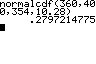
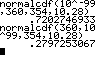
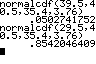
μ = 354 und σ = 10,28 P(360≤X≤400) P(X ≤ 360) P(360 ≤ X) |
|
|
|
n=500 und p=0,7 P(X ≤ 360) P(360 ≤ X) |
|
|
Normalverteilung (ganzzahliges Merkmal, Stetigkeitskorrektur)
|
μ = 35.4 und σ = 3,76 P(X=40) P(30≤X≤40) |
|
|
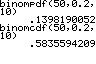
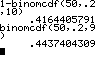
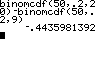
 und
und

 L1 L2
L1 L2

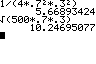
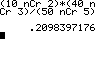
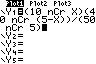

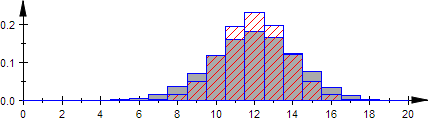 N=50, M=30, n=20
N=50, M=30, n=20
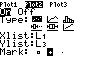

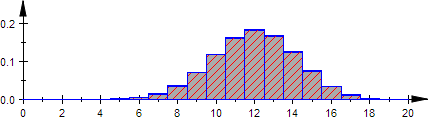 N=500, M=300, n=30
N=500, M=300, n=30