Eike Teiwes

Beschreibung geometrischer Objekte

package("geo"): export(geo):

Wir unterscheiden Punkte und Vektoren, die MuPAD durch Listen bzw. Matrizen beschrieben werden.

[1,2,3], matrix([1,2,3])


                                          +-   -+
                                          |  1  |
                                          |     |
                               [1, 2, 3], |  2  |
                                          |     |
                                          |  3  |
                                          +-   -+

Zunächst aus Bequemlichkeit wird eine Prozedur punkt eingeführt, die unterschiedliche Eingaben akzeptiert und
daraus die Koordinaten extrahiert.

punkt(1,2,3), punkt(vektor(1,2,3)), punkt(matrix([1,2,3])), punkt([1,2,3])

Entsprechend wird eine Prozedur vektor eingeführt.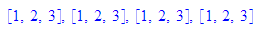

vektor(1,2,3), vektor([1,2,3]), vektor(matrix([1,2,3])), vektor(vektor(1,2,3))

Wie man sieht bieten die beiden Prozeduren eine Umwandlung der Objekttypen Punkt und Vektor.

Eine Gerade wird beschrieben durch

matrix([1+r,r,r])

Wieder wird eine Prozedur gerade eingeführt, die unterschiedliche Beschreibungsgformen einer Gerade nachbildet.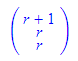

gerade(1+r,r,r),                        // Vektorform
gerade(vektor(1,0,0)+r*vektor(1,1,1)),  // Parameterform
gerade(vektor(1,0,0),vektor(1,1,1)),    // Orts-Richtungvektor-Form
gerade(punkt(1,0,0),vektor(1,1,1)),     // Punkt-Richtungs-Form
gerade([1,0,0],[2,1,1])                 // Zwei-Punkte-Form

Da die üblichen Rechenregeln für Matrizen gelten, kann eine Gerade auch so definiert werden: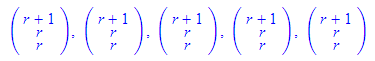

vektor(1,0,0)+r*vektor(1,1,1)

Und schließlich gibt es zur einfachen Beschreibung einer Ebene auch eine Prozedur ebene.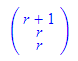

ebene(2-2*s,r+s,r+2*s),                                // Vektorform
ebene(vektor(2,0,0)+r*vektor(-2,1,2)+s*vektor(0,1,1)), // Parameterform
ebene(vektor(2,0,0),vektor(-2,1,2),vektor(0,1,1)),     // Orts-Richtungsvektor-Form
ebene([2,0,0],[0,1,2],[2,2,2]);                        // Drei-Punkte-Form
ebene(vektor(1,-2,2),vektor(2,2,2)),                   // Normalenform
ebene(x-2*y+2*z=2);                                    // Koordinatenform

Irgendeine Ebene? Irgendeine Gerade in der Ebene? Zwei Punkte auf der Gerade? Kein Problem: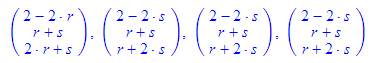

E_ := ebene(); g_ := gerade(E_); punkt(g_), punkt(g_);

Während vektor() wie erwartet einen zufällligen Ortsvektor liefert, ergibt vektor(E_) oder
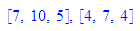
vektor(g_) einen zufällligen Richtungsvektor der Ebene bzw. Gerade.

vektor(), vektor(E_), vektor(g_)

Auch zweidimensionale Anfragen sind möglich.

vektor(2) $i=1..5;
vektor(gerade(2,1-r)) $i=1..5;
punkt(gerade(2,1-r)) $i=1..5;

Wie gezeigt wandeln punkt und vektor eineinander gegenseitig um.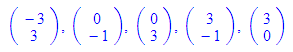
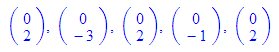
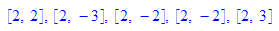
Wie gelangt man nun an die die bestimmenden Vektoren einer Gerade?

ortsvektor(gerade(1+r,r,r)),
richtungsvektor(gerade(1+r,r,r))

Entsprechend erhalten wir einen Ortsvektor und zwei Richtungsvektoren einer Ebene, und auch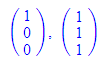
einen Normalenvektor:

ortsvektor(ebene(2-2*s,r+s,r+2*s)),
richtungsvektor(ebene(2-2*s,r+s,r+2*s)),
normalenvektor(ebene(2-2*s,r+s,r+2*s))

Auch die Umwandlung einer Ebenenform in eine andere gelingt.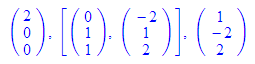
ebene selbst führt alle Eingaben die Matrixdarstellung (Vektordarstellung) über.

ebene(2-2*s,r+s,r+2*s);
p2n(%);
n2k(vektor(-1,2,-2),vektor(2,0,0));
k2p(-x+2*y-2*z+2=0);
% | {r=t,s=u};
% | {t=2-2*r,u=r+s}

Die beiden letzten Anweisungen zeigen, dass es sich am Ende um die ursprünglich gegebene Ebene handelt.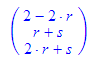
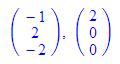
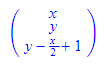
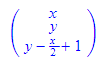
Auch die explite Darstellung in Parameterform oder Normalform ist möglich.

E_ := ebene(2-2*s,r+s,r+2*s);
PF(E_);
NF(E_);
KF(E_);
AF(E_);

Die Darstellung in Parameterdorm bzw. Normalenform dienst zunächst der Lesbarkeit.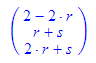
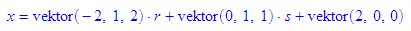
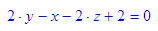
ebene akzeptiert diese Ausgabe aber auch als Eingabe.

hold(vektor(2,0,0)+r*vektor(-2,1,2)+s*vektor(0,1,1));
ebene(%); // PF
hold(skalarprodukt(vektor(-1,2,-2),x)=-2);
ebene(%); // NF

Und mit beiden Darstellungsformen kann "gerechnet" werden:
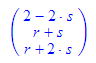
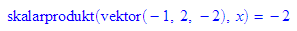
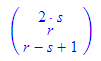
Aus der Normalenform wird die Hessesche Normalenform entwickelt.
Es kann unmittelbar duurch Einsetzen geprüft werden, ob ein Punkt oder Vektor zur Ebene gehört.
Auch der Schnitt von Ebene und Gerade ergibt sich durch Einsetzen in die Normalenform.
Und schließlich kann die Normalform wieder in die vektorielle Form gebracht werden.

NF(E_);
NF(E_) / betrag(normalenvektor(E_));
NF(E_) | x=vektor(1,2,3);
NF(E_) | x=gerade(1,r,1-r); // als ...
gerade(1,r,1-r) | solve(%); // ... Zweizeiler
gerade(1,r,1-r) | solve(NF(E_) | x=gerade(1,r,1-r)); // als Einzeiler

Ähnlich kann mit der Parameterform gearbeitet werden. Jedoch ist PF(E_) eine "eindimensionale Beschreibung".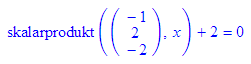
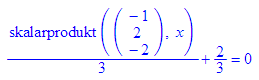
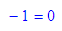
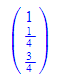
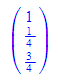
Erst bei einer ausdrücklichen oder impliziten Auswertung tritt die Vektorschreibweise hervor.
Durch eval(PF(E_))[2] oder eval(PF(E_)[2]) erhält man einen Ebenenvektor.

PF(E_);
eval(PF(E_));
PF(E_) | r=2;
PF(E_) | {r=0,s=0};
eval(PF(E_))[2], eval(PF(E_)[2])

Für die grafische Darstellung wird die Bestimmung der Spurpunkte bzw. der Spurgeraden in den Koordinatenebenen wichtig sein.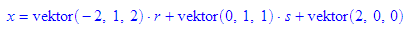

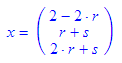
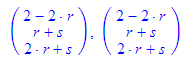
spur(gerade(vektor(1,0.5,1),vektor(1,-2,0)));
spur(ebene(vektor(2,1,2),vektor(3,2,1)))

Wie auch die Bestimmung der Achsenabschnitte.

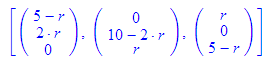
abschnitt(ebene(vektor(2,1,2),vektor(3,2,1)));
abschnitt(gerade(vektor(1,2),vektor(1,-2)));

Wie die letzte Anweisung zeigt, sind alle Prozeduren so ausgelegt, dass auch Beschreibungen und Berechnungen im R2
möglich sind.

Einige Hilfprozeduren erleichtern die Untersuchungen:
istPunkt und istVektor prüfen den Objekttyp, wobei Gerade und Ebene als "freie" Vektoren mit Parametern
hier nicht als Vektor angesehen werden.

istPunkt([1,2,3]),istPunkt(vektor(1,2,3)),istVektor([1,2,3]),istVektor(vektor(1,2,3));
istGerade(gerade(r+1,r,r)), istEbene(gerade(r+1,r,r));

Geraden und Ebenen werden von den Prozeduren istGerade und istEbene erkannt.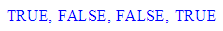
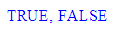
Die Prozeduren parameter und parameteranzahl assistieren dabei.

g_ := gerade(1+r,r,r):
E_ := ebene(2-2*s,r+s,r+2*s):
parameter(g_), parameteranzahl(g_), istGerade(g_);
parameter(E_), parameteranzahl(E_), istGerade(E_);